nominalアプローチの "nominal" の訳語について考える
計算機科学の分野において nominal set や nominal logic に現れる "nominal" は「名前の具体的な値を切り捨て、置換と有限supportによって構造を記述する方法」を表します。 nominalアプローチを用いると、例えばα変換を群論の言葉 (群作用など) を使って非常に見通しよく定義できます。
この意味で使われる "nominal" には今のところ定まった訳はありませんが、J-GLOBALでは『名目』および『公称』として訳されているようです1 (ソース1、ソース2)。 しかし、これらの訳はいくつかの理由 (「名前に関する」という意味が弱い、など) から、nominalの訳語としてはベストなものとは言い難いと考えられます。
そこで、本記事では「置換と有限supportによる構造を記述する方法」の "nominal" の訳語として、統計学の名義尺度 (nominal scale) を参考にした『名義』という訳を提案したいと思います。
この記事はほとんど筆者の手で執筆し、事実関係の確認もしましたが、一部文章の校正などを生成AI (Gemini, ChatGPT) によって行なっています。
nominalアプローチとは
はじめに、計算機科学におけるnominalアプローチについて簡単に説明します。 この辺りはかなり専門的なので、難しそうなら次の一文だけ覚えて、続くセクションに移っていただいて構いません。
nominalアプローチは「名前の具体的な値を切り捨て、置換 (permutation) と有限supportによって構造を記述する方法 (approach)」のことです。
nominalアプローチの紹介として、nominal abstract syntax と呼ばれるものを用いて、α変換や自由変数を記述する方法を説明します。
そのためにまず、nominalアプローチやnominal abstract syntaxの言葉をいくつか導入します。
- nominalアプローチでは変数名のことをatomと呼び2、その (可算無限な) 集合を で表します。
- λ項とは構文 で定義されるものです ( はatom)。
- λ項 の中の変数 (atom) を置換 で置き換えたものを と表すことにします。 これは群論の言葉で言うと、置換 のλ項 への (左) 作用になります。
- atomの集合 がλ項 について次の性質を満たすとき、 を のsupportと呼びます:
例を挙げて説明します。
- はatomです。
- λ項 とします。このとき、
- と を入れ換える置換 を作用させると となります。
- と を入れ換える置換 を作用させると となります。
- 集合 はλ項 のsupportとなります。
nominalアプローチで最も重要なのは、扱う対象が必ず有限support (大きさが有限のsupport) を持つと仮定することです。 これはプログラミング言語を扱う場合には自然な仮定となります。 なぜなら「プログラムに含まれる変数名はatom」であり「プログラムの大きさは有限なので、出てくる変数名の個数も当然有限」だからです。
このsupportと置換の概念を使うと、α変換 は次のように定義できます。
定義 (α変換):
ここで、 はλ項 と のsupportに含まれず引数の でも でもない (フレッシュな) atomで、 と は および と を入れ換える置換です。 supportの大きさが有限な一方で、atom全体 の大きさは可算無限なため、フレッシュなatomは必ず取れます。
注目してほしいのは、ここまでで自由変数や束縛変数のような言葉を一切導入せず、α変換が定義できている点です。 通常、α変換というと自由変数や束縛変数の扱いがややこしく問題となります。 しかし、そういった面倒な概念を導入せず置換とsupportのみでα変換を定義できることから、nominalアプローチの筋の良さが感じられると思います。
さらにすごいところは、これを拡張して自由変数や束縛変数の概念まで表現できてしまうことです:
- 2つのλ項 と がα同値 () だとします。
- この関係性は任意の置換 で保存 () されます。
- λ項全体からなる集合を として、この集合をα変換 で割った商空間 を考えます。
- で割っているため、同値類 のsupportは、元のλ項 の自由変数の集合に一致します4。
- よって、λ項 のsupportから のsupportを除いた差集合は束縛変数の集合となります。
ここまで説明した置換を用いたλ項の扱いは、Gabbay & Pitts (2002) の "A New Approach to Abstract Syntax with Variable Binding" という論文で導入されたもので、nominal abstract syntax や nominal term と呼ばれています。
この「置換と有限supportによって名前を持つ構造を記述する」という方法はnominalアプローチとして定式化され、計算機科学の様々な分野へと応用されています。 例えば、次のような応用が知られています:
- nominal logic
- nominal unification / nominal rewriting
- nominal automata
nominalアプローチは今日の計算機科学の分野において重要な概念となっています。 ですが、この意味での "nominal" には、まだ定まった日本語訳が存在しません。 本記事では、この問題に対して一つの解答を提示したいと思います。
"nominal" の訳語の模索
ここからはnominalアプローチの "nominal" の訳語を考察して、適切な訳語を模索していきます。 以降、次のような順序で考察を進めていきます。
- 辞書での "nominal" の意味・訳を調査し、訳語の候補を絞り込む
- →『名義』と『名目』が候補として挙がる
- 他分野での "nominal" の使われ方の調査し、どの訳がより適しているか考える
- 『名目』は定量的な用語に使われるけれど、『名義』は定性的な用語に使われる
- → 『名義』が良さそう
- 統計学の『名義尺度』との興味深い関連性を見つけたので、その紹介
- 「置換によって特徴付けられる名前」という共通点がある
- → この関係性は本質的なので『名義』と訳すべき
辞書での "nominal" の意味・訳
訳を考える際に、最初に行うべきことは辞書を確認して、その単語の意味を調べることです。 さらに、実際にどのような訳語が使われているかを整理し、どの訳語を使うと期待の意味になるのかを考えます。
というわけで、weblio英和辞典と英辞郎での意味を確認しました。 辞書の内容をそのまま載せることはあまり良いことではないので、2つの辞書の内容を要約すると、形容詞 "nominal" には大きく分けて次のような意味があるようです。
形容詞 "nominal" の意味:
- 名前の、名前に関する
- 名詞の
- ほんのわずかな
- 額面通りの
他にも細かな意味はいくつかあるようですが、これらの意味を細分化したものと考えられると思います。
nominalアプローチの "nominal" には、これらのうちどのような意味を重視しているでしょうか。 私見ですが、このニュアンスが特に重要です:
変数名 (atom) を扱うため「1. 名前の、名前に関する」というニュアンスが明確でなければいけない
次に、どのような訳が良いのかを検討するために、既存の訳語の整理します。 英辞郎の検索結果で出てきた熟語の訳をまとめたところ、次のような訳が "nominal" に対して使われていることが分かりました。
- 『公称』 (公称回転角度 nominal angle of rotation、公称エネルギー nominal energy)
- 『名目』 (名目勘定 nominal account、名目年率 nominal annual rate)
- 『額面』 (額面価額 nominal amount、額面価格 nominal par)
- 『微量』 (微量抗原 nominal antigen)
- 『名詞』 (名詞失語症 nominal aphasia、名詞節 nominal clause)
- 『呼び』 (ボルト呼び径 nominal bolt diameter、呼び容量 nominal capacity)
- 『表面』 (表面利率 nominal coupon)
- 『唯名』 (唯名的定義 nominal definition)
- 『(ごく、ほんの) わずかな』 (ごくわずかな料金 nominal fee)
- 『名』 (名簿 nominal list)
- 『定格』 (定格負荷 nominal load)
- 『基準』 (基準寸法 nominal measurement)
- 『名義』 (名義株主 nominal owner、名義尺度 nominal scale)
- 『体言』 (体言文 nominal sentence)
- 『標準』 (標準軌道 nominal trajectory)
さきほど挙げた条件を意識すると、『名義』と『名目』 の2つが候補として挙げられます。 具体的には、次のような理由があります。
『名義』と『名目』は『名』という漢字が含まれていて「1. 名前の、名前に関する」ことが明らかである (『名詞』と『唯名』も同様だが、これらは特定の分野、すなわち言語学と哲学の印象がつよい)
それでは、どちらがnominalアプローチの訳により適しているのでしょうか。
"nominal" の意味を掘り下げるために、他のアカデミックな分野での "nominal" について分析していきたいと思います。
他分野での "nominal" の使われ方
アカデミックの基本は「巨人の肩に乗る」ことです。 というわけで、先行研究として他のアカデミックな分野での "nominal" という単語の使われ方について調査・分析し、nominalアプローチの "nominal" と関連するものが無いか探していきます。
さきほど確認したように "nominal" は多義的な英単語で、アカデミックな文脈でもいくつもの意味があります。 ただ幸運なことに、それぞれの分野での意味にそこそこ別の訳語が割り当てられているため、分類は難しくありません。
- 哲学: 『唯名』
- 言語学: 『名詞』
- 経済学: 『名目』
- 工学: 『公称』、『呼び』
- プログラミング言語: 『名前的』、『公称』
- 生物学: 『名義』
- 統計学: 『名義』
これらについて順番に説明していきます。 ただし、基本的にこれらの分野については自分は専門家ではないため、間違っているところがあったら申し訳ありません。
1. 哲学: 『唯名』
哲学の唯名論は英語では nominalism と呼びます。
「(赤い) りんご」や「(赤い) バラ」のような実在するものに対して、「赤」のような普遍的な概念は実在せず、実在するものを指すラベル (名前) である、という形而上学上の立場です。 対義語は実在論 (realism) とされています。
世界には名前しか無いという極端な立場ではないことに注意してください (普遍的なものは名前としてのみ在るという立場だと理解しています)。 哲学についてはそこまで明るくないのでこれくらいにしておきます。
2. 言語学: 『名詞』
言語学の分野では、文法用語として "nominal" は名詞に関係する語を表すために用いられます。
例えば nominalization は名詞化と、nominal phrase は名詞句、nominal style は名詞構文と訳されます。 この意味のnominalに直接の対義語はありませんが、関連する語 (形容詞) としては verbal (動詞の〜) などがあります。
3. 経済学: 『名目』
経済学では "nominal" は『名目』と訳され、『実質 (real)』とセットで使われます。 代表的な例として名目GDP (nominal GDP) と実質GDP (real GDP) や名目賃金 (nominal wage) と実質賃金 (real wage) が挙げられます。
ここでの "nominal" (名目) は、「貨幣の額面通りの」という意味を持ちます。 例えば、給料の金額そのものは「名目賃金」ですが、物価の変動を考慮して「実際にどれだけの物が買えるか」を表すのが「実質賃金」です。 もしインフレで物価が上がれば、名目賃金が変わらなくても、実質賃金は下がることになります。
つまり、この分野における "nominal" は辞書の「3. ほんのわずかな」や「4. 額面通りの」という意味を煮詰めたようなものになっています。 また、英辞郎ではこの方向性での訳として『表面』や『額面』も見られました。
4. 工学: 『公称』、『呼び』
工学においては、nominalを『公称』と、また産業分野では『呼び〜』などと訳します。 英辞郎では他に『基準』や『標準』という訳も見られました。 これらの指すところは同じで「理論上・規格上の数値」という意味になります。
対義語は『実測』や『有効』です。 英語では actual や effective で、次のような対義語のペアがあります。
- 公称値 (nominal value) ⇔ 実測値 (actual value)
- 呼び径 (nominal size) ⇔ 実寸 (actual size)
- 呼び径5 (nominal diameter) ⇔ 有効径 (effective diameter)
nominalな値はあくまで規格上の数字なので、規格の互換性について話すときなどのみに使い、実際の設計作業の際にはactual・effectiveな値を使う、といった使い分けをするようです。
この意味での面白い表現としては、SF映画などで "all systems nominal" と言ったら「システムは正常だ (すべてのシステムは仕様通りに動いている)」みたいな意味になるらしいです。 こちらも「4. 額面通りの」という意味から派生していると思うのですが、かなりポジティブな意味に捉えられているように思います。
5. プログラミング言語: 『名前的』、『公称』
プログラミング言語の分野では nominal type system という用語があり、この訳として名前的型システムもしくは公称型システムが知られています。
Javaなどの型システムで使われている「名前が重要で、部分型関係が明示的に宣言される型システム」6をnominal type systemと呼びます。 対義語は構造的型システム (structural type system) です。
名前的型システムはTAPL (Types and Programming Languages) の日本語訳「型システム入門」で使われている訳です。 一方、公称型システムや公称型付け (nominal typing) という言葉はTypeScriptなどのプログラマのコミュニティでよく使われているように思います。
6. 生物学: 『名義』
生物学では "nominal" を『名義』と訳します。
生物学 (とくに分類学) では名義タクソン (nominal taxon)や名義種 (nominal species)のように使われます。 これらは、その分類が生物学的に正しい (有効である) かどうかにかかわらず、命名規約に従って定義された「名前としての存在」 を指すために用いられます。 対義語は『有効な (valid)』か『分類学的 (taxonomic)』です。
7. 統計学: 『名義』
統計学でも "nominal" を『名義』と訳します。
統計学では "nominal" は尺度水準 (level of measurement) の一種の名義尺度 (nominal scale) として現れます。 名義尺度とは、アンケートの項目における性別や、電話番号、住所のような、「値が等しいか・異なるか」だけに意味があるもの で、値の間に大小関係のような他の関係が無いものを指します。 また、名義尺度とほぼ同じ意味の言葉として名義変数 (nominal variable) もあります。 この意味での対義語は他の尺度水準の順序水準 (ordinal scale) です。
他分野での使われ方のまとめ
ここまでの調査を表にまとめたものが以下になります。 この表で『名義』と『名目』のどちらが良さそうかを分析します。
| 訳語 | 分野 | ニュアンス | 対義語 | 名前との関連性 |
|---|---|---|---|---|
| 『唯名』 | 哲学 | 普遍的概念についての哲学的立場 | 『実在 (real)』 | ✔ |
| 『名詞』 | 言語学 | 文法用語としての名詞 | 『動詞の (verbal)』 など | ✔ |
| 『名目』 | 経済学 | 実質を伴わない、表面上の数量 | 『実質 (real)』 | |
| 『公称』、『呼び』 | 工学 | 理論上・規格上の数量 | 『実測 (actual)』 など | |
| 『名前的』、『公称』 | プログラミング言語 | 宣言された名前による部分型 | 『構造的 (structural)』 | ✔ |
| 『名義』 | 生物学 | 命名規則に従って定義された名前 | 『有効な (valid)』 など | ✔ |
| 『名義』 | 統計学 | 等価性だけに意味がある名前 | 『順序 (ordinal)』 | ✔ |
前のセクションで「1. 名前の、名前に関する」というニュアンスが明確であることが重要だと述べました。
しかし調査の結果、アカデミックな分野、とくに経済学において『名目』は、名前との関係性が希薄な、数量に関する (定量的な) 語として扱われていることが分かりました。 そのため、『名目』はnominalアプローチの "nominal" の訳には適さない、と結論付けられます。
また、『名目』という言葉は、私たちが直感的に想像する以上に経済学の意味に支配されているのではないか、という予想が自分の中にあります。 これは表の中で『名目』を使っているのが経済学しか無いことに加えて、Google検索で『名目』と検索すると、1つを除いて全てで「経済学での名目と実質」に関連するWebページが表示される7ことが理由として挙げられます。 単に『名目』と検索しただけでこの検索結果となるのは、如何にこの訳が経済学と深く結び付いているかを物語っています。 そのため『名目』という訳を経済学以外の分野で使うのは、不要な混乱を産むように思います。
この表をよく見ると、新たな "nominal" の訳語の候補としてプログラミング言語の分野の『名前的』と『公称』も考えられることが分かります。 しかし、これらも訳語には次のような問題があります。
- 名前的型システム (nominal type system) はnominalアプローチとは関係がありません。
- nominalアプローチでは名前は「宣言されるもの」ではないため、全く異なる概念だと分かります。
- 実際にこれらの研究を見比べてみても、これらを関連付けて論じていることはありません。
- そのため意味の衝突が起こってしまいます。これを避けるために、別の訳語にするべきです。
- 分野が近過ぎるが故の問題だと思います。
- 英語では既にややこしい状況ですが、日本語では訳を分けることで衝突を避けられるはずです。
これらを踏まえた上で、nominalアプローチの "nominal" を『名義』と訳すことについて考えます。 この訳の借用は生物学と統計学の慣習に従ってもそれほど問題では無さそうで、とくに「1. 名前の、名前に関する」というニュアンスは生物学・統計学のどちらの使い方でも明確です。
よって、他分野の既存の訳語の比較により「nominalアプローチの "nominal" の訳は『名義』が良さそうだ」と分析できました。
ですが、話はここで終わりません。 実は、こうした相対的な理由だけでなく、より本質的な・絶対的な理由が、統計学での名義尺度とnominalアプローチの間には存在します。
名義尺度とnominalアプローチの関係性
最後に、統計学の名義尺度とnominalアプローチが「置換によって特徴付けられる名前」という共通点を持っていることについて説明します。 この関係性によりnominalアプローチの "nominal" を『名義』と訳すのがきわめて自然なことだということが分かるはずです。
さて、名義尺度はよく「値に大小関係がなく、等しいか異なるかだけで区別できるもの」という説明をされますが、厳密にはどのように定義されるのでしょうか?
その答えは、尺度水準を導入した原論文である、S. S. Stevens (1946) の "On the Theory of Scales of Measurement" で述べられています。
Stevensの仕事について確認する前に一旦、尺度水準とは何かを確認しましょう。 尺度水準とは、統計学で使う尺度 (scale) の分類水準で、原論文では次の4種類が提案されました。
定義: 尺度水準 (level of measurement) とは、次の4種類の尺度である。
- 名義尺度 (nominal scale): 値に大小関係がなく、等しいか異なるかだけで区別できるもの (例、性別や電話番号など)
- 順序尺度 (ordinal scale): 値を大小関係で区別できるが、どれくらいの差があるかは分からないもの (例、藤田スケールやモース硬度など)
- 間隔尺度 (interval scale): 値の間の差が分かるもの、つまり値の間の加減が意味を持つもの (例、カレンダーの日付やセ氏や華氏で表された温度など)
- 比率尺度 (ratio scale): 値の間の加減乗除が意味を持つもの (例、年齢や絶対温度など)
名義尺度は定性的 (qualitative) ですが、他の3つは定量的 (quantitative) です。 また、これらの尺度には階層関係があり、高い水準の尺度は低い水準の尺度を含んでいて、高い水準のデータを低い水準のデータに変換して扱うことができます。
では、Stevensはこれらの尺度をどのように特徴付けて、階層関係があるといったことを結論付けたのでしょうか?
Stevensはこの問題に群論の言葉を用いて取り組みました。 実際に原論文を見ると、次のような表 (原論文ではTable 1) があります。
| Scale | Basic Empirical Operations | Mathematical Group Structure | Permissible Statistics (Invariantive) |
|---|---|---|---|
| Nominal | Determination of equality | Permutation group means any one-to-one substitution | Number of cases Mode Contingency correlation |
| Ordinal | Determination of greater or less | Isotonic group means any monotonic increasing function | Median Percentiles |
| Interval | Determination of equality of intervals or differences | General linear group | Mean Standard deviation Rank-order correlation Product-moment correlation |
| Ratio | Determination of equality of ratios | Similarity group | Coefficient of variation |
今回重要なのは "Mathematical Group Structure" / "Nominal" の項目です。 ここには "Permutation group " および " means any one-to-one substitution" とあります。
ここで、計算機科学と統計学という異なる分野で使われていた "nominal" が「置換によって特徴付けられる名前を扱う方法」として結び付けられました。
この事実は、名義尺度とnominalアプローチが、単純に意味が似ているというたけではなく、より本質的なところでつながっていることを表しています。
ここで、名義尺度をnominalアプローチの言葉で考えてみましょう。
- 名義尺度の1つのデータはatomに相当します。
- 例えば血液型の「A型・B型・AB型・O型」という選択肢は名義尺度です。
- そのため、個々の項目「A型」「B型」「AB型」「O型」はatomです。
- 統計分析に使う名義尺度のデータセットの大きさは有限です。
- したがって、出現する名義尺度のデータ (atom) の種類も有限になるはずです。
- よって、「名義尺度のデータセット」は有限supportを持ちます。
- そのため統計分析にnominalアプローチを応用することができます (!!)。
nominalアプローチの理論的基礎として nominal set があります。 これはnominalアプローチの重要な性質 (各元が有限supportを取る) を満たすような集合のことで、例えば最初の例のλ項全体の集合 や、それをα変換で割った商空間 はnominal setです。
この意味で、「名義尺度 (nominal scale) のデータセット全体の集合はnominal setである」と主張することは、決して間違いではないと考えています。
さらに、もっと強気な主張をするのなら、次のようなことも言えるはずです。
統計学の名義尺度とは、計算機科学のnominalアプローチの一種である。
流石に現時点では、この主張は少し無理があるかもしれません。 しかし、このように考えることで、統計学と計算機科学を結び付ける新たな研究領域が開拓される可能性は十分にあります。 そして、その研究が進んでいけば、この主張が自明に真となる日もくるかもしれません。
このように、nominalアプローチと統計学の名義尺度 (nominal scale) は理論的背景のレベルで深くつながっており、訳語は共有されるべきだ、というのがこの記事での自分の主張になります。
nominalアプローチ改め名義アプローチ
ここまでの議論を通して私は、nominalアプローチの "nominal" を『名義』と訳すべきだと結論付けます。
早速使ってみましょう。
- 名義アプローチ (nominal approach)
- 名義集合 (nominal set)
- 名義抽象構文 (nominal abstract syntax) / 名義項 (nominal term)
- 名義論理 (nominal logic)
- 名義単一化 (nominal unification) / 名義書き換え (nominal rewriting)
- 名義オートマトン (nominal automata)
そこまで悪くない気がします。
ただ「名義書き換え」は後に続く語が一般的すぎてアカデミックな意味を失なって「名義 (名前) を書き換えているだけ」のように読めてしまいます。 こういうときは語を補なって「名義項書き換え」や「名義的書き換え」とするといいのではないかと思います。
何はともあれ、名義の語感がそこまで悪くなさそうで良かったです。

nominalの訳は「名義」に決定!
「名義アプローチ」を使っていきましょう!
メモランダム
"nominal" の適切な訳語を調査している際に感じたことや分かったことなどのうち、上手く本体の文章にまとめられなかったものをメモとして残しておきます。
FM集合論と「名目」
FM (Fraenkel-Mostowski) 集合論は名義アプローチの基礎となっている集合論です。 これは元々、選択公理 (Axiom of Choice) がZF (Zermelo-Fraenkel) 集合論の他の公理に独立していることを示すために考案されたものです。
FM集合論の中で原子 (atom あるいは urelement) は、公理による集合の構成法 (空集合からの構成) とは独立して存在するものとして与えられます。 つまり、原子は集合論の対象として扱われるものの、本来の集合としての実体を持たない、いわば「名目上の集合」と解釈できるわけです。
このFM集合論での原子の扱いを考えると "nominal" を『名目』と訳すことはあながち間違いではないように思えます。 しかし、名義アプローチはこのFM集合論の原子に、プログラミング言語での変数名としての意味を見出したことで生まれた概念なので、因果関係が逆転しています。 そのため、やはり『名目』は適切ではなさそうです。
生物学における "nominal" の翻訳の歴史
生物学 (分類学) において「"nominal" をどう訳すべきか」というのは1980年代に議論があったようです。 このことは伊藤 立則「<研究‧技術報告> 国際動物学命名規約 第3版について」 (1989) という報告書 (PDF) で見られます。 また、現在のnominalの訳も依然として『名義』であることは「国際動物命名規約 第4版」 (1999) の日本語版 (PDF) で確認できます。
これらの文献によると、かつては生物学の分野で "nominal" は『公称』と訳されていたようです。 しかし、報告書の著者の伊藤はこの『公称』という訳について次のように述べています。
旧訳ではこれを「公称」とし,「公称属」とか「公称種」のようにして使われていた。 筆者は,「公称」という日本語からくる印象と"nominal"が本当に意味するところのものが一致していない,と長いこと感じていた。 『公称』と言うと,別に通称や俗称があって,それらと違う公に認められた名称を指しているように思える。
そして『nominal taxonとは,分類学的単元 (taxonomic taxon) に対比される概念』として、『nominal taxonは,名称上の単元で,その単元の内容 (例えば,形態・分布など) や他の単元との境界などを問わない』ため『nominal taxonの“nominal"の意味は,日本語で「名義上の」と言うのにほぼ等しい』としてnominalを「名義」と訳すことを提案しています。
この生物学での歴史で、今回の議論において興味深い点は次の2つです。
1. taxonomic taxonについて
伊藤は分類学的単元 (taxonomic taxon) について『名前がついている単元あるいは個体を含み,ある境界で他の分類学的単元から区別できるものである (区別できるようにしようとしている)』と述べています。 これは一見するとnominalアプローチでの名前について言っているように聞こえます (「区別できる」などのキーワードがとくにそう見えます) が、そうではありません。 この主張はtaxonomic taxonでは、生物学的な「中身」を見なければ適切な名前を選ぶことができない、ということを言っていると自分は理解しています。 つまり、taxonomic taxonでは名前は単なるラベル以上の意味を明確に持っているわけで、これはnominalアプローチとは正反対の名前の扱いとなっています。
ここからは自分の推測ですが、生物学・分類学においてどうしてこのような名前の分類が必要になるのかというと、生物が発見されたときにその場所などから命名規則を使って付けられる学名と、実際に生態などを分析した結果発見された本来付けるべき学名の2種類があり、これらが乖離することがあるからではないかと思います。 ここで、前者をnominal taxonと呼び、後者をtaxonomic taxonと呼ぶわけです。 こういった命名法や分類については、計算機科学や数学をやっている身では中々想像が付きませんが、共通する単語を通じてわずかに触れることができました。
2. "nominal" の訳の難しさ
今まさに我々が計算機科学の分野で行おうとしている「"nominal" の訳語についての議論」が、1980年代の日本の生物学の分野でも行われていた、という事実は非常に示唆に富んでいます。 繰り返しますが、英単語 "nominal" の意味は多岐に渡り、一つの日本語に割り当てきれるものではありません。
完全に私見ですが、『公称』や『名目』という単語はいかにも学術的な響きがあり8、アカデミックな文脈で "nominal" の訳に割り当てられやすいのではないかと思います。 しかし、その意味は日本語としてはやや限定的だったり、特定の分野での利用が支配的だったりします。 この点に疑問を持ち、代替案を提案し定着した歴史が過去にある、というのは今回の議論を積極的に進める動機にもなります。
哲学と経済学における "nominal" の対義語 "real" の違い
様々な分野で "nominal" の訳語を比較した際に、哲学と経済学での "nominal" の訳はそれぞれ『唯名』と『名目』で、その対義語は『実在』と『実質』です。 そして、これらに対応する英語はどちらも "real" でした。 しかし、哲学と経済学における "nominal" と "real" の関係の意味するところは対照的です。
哲学のrealismが「抽象的な概念の実在」を主張するのに対し、経済学の "real" は「具体的な物 (購買力)」を指します。 同じnominal / realという構図でありながら、見ている世界が逆転しているのは興味深い点です。
このようになるのは "nominal" や "real" が哲学では普遍的概念 (universal) に対して係っていて、経済学では 価値 (value) に対して係っているからだと考えられます。 哲学の実在論 (realism) は、プラトンのイデアのように「目に見えない抽象的な概念こそが真実 (real) である」と説きます。 一方で、経済学の実質 (real) は、「お金という抽象的な数字 (nominal) ではなく、実際に交換できる物 (real) こそが真実である」という立場です。
つまり、哲学では「抽象」こそがreal であり、経済学では「具象」こそがreal なのです。 同じ "real" という言葉を使いながら、真逆の方向を向いている点にアカデミックな用語の面白さを感じます。
nominal type (名前的型あるいは名義型) について
プログラミング言語の分野では名前的型システムもしくは公称型システム (nominal type system) という概念があることは、さきほど述べた通りです。 しかし、名義アプローチを型理論に応用した (dependent) nominal type theory (今回の訳では (依存的) 名義型理論) という研究が存在しています (例えば[Cheney (2012)]など)。
この2つは全く異なる型について扱っています (名前的型システムはJavaのような宣言と名前による部分型で、名義型理論は名義論理 (nominal logic) とCurry-Howard対応がある型)。 ですがnominal typeという語が共通しているため、かなりややこしいです。 一応、名義型理論は依存型 (dependent type) の文脈で出てくるため、知識があれば文脈で区別することはできるようになっているみたいです。
名義アプローチの用語の訳
PLでのnominalにはいくつか関連する用語 (atomやsupport) があります。 今回は訳語について議論する記事なので、これらの用語も訳さずそのままの単語を使っていましたが、実際には訳した方がいいと思います。
その訳として個人的には、atomは原子で、supportは台もしくは台集合で良いと考えています。 原子 (atom) については公理的集合論での定訳なので、敢えて変える必要は無いと思っています。 supportも解析学の台 (support) に類似する概念なので同じ言葉を使うか、少し補足して台集合とすると良いのではないか、という考えです。
名義アプローチの訳の現状
最後に、名義アプローチの "nominal" の日本語訳が現状 (2026年1月) どうなっているのかについて、簡単に説明します。
まず、記事の冒頭で述べた通り、J-GLOBALではnominalの訳として主に『名目』と『公称』そしてカタカナの『ノミナル』の3種類が選ばれているようです。 おそらくほとんどが機械翻訳されたもので、一つの論文のタイトル・アブストラクトの中にこれらが混ざっていることも多々あります。 参考までに、いくつかのキーワードで検索した結果の件数を記録しておきます。
- 「名目集合」41件 (検索ページ)
- 「名目論理」10件 (検索ページ)
- 「公称集合」25件 (検索ページ)
- 「公称論理」 8件 (検索ページ)
- 「ノミナル集合」 8件 (検索ページ)
- 「ノミナル論理」 2件 (検索ページ)
はっきり言って機械翻訳なのでそこまでの権威は無いと思うのですが、日本語設定で "nominal set" でGoogle検索すると上位に出てくる検索結果にJ-GLOBALのページが出てきたり、Google検索で勝手に生成されるAI要約で「名目集合」という訳が出てくるので、初学者が "nominal set" の訳は「名目集合」なんだな、と誤解してしまう可能性があります。
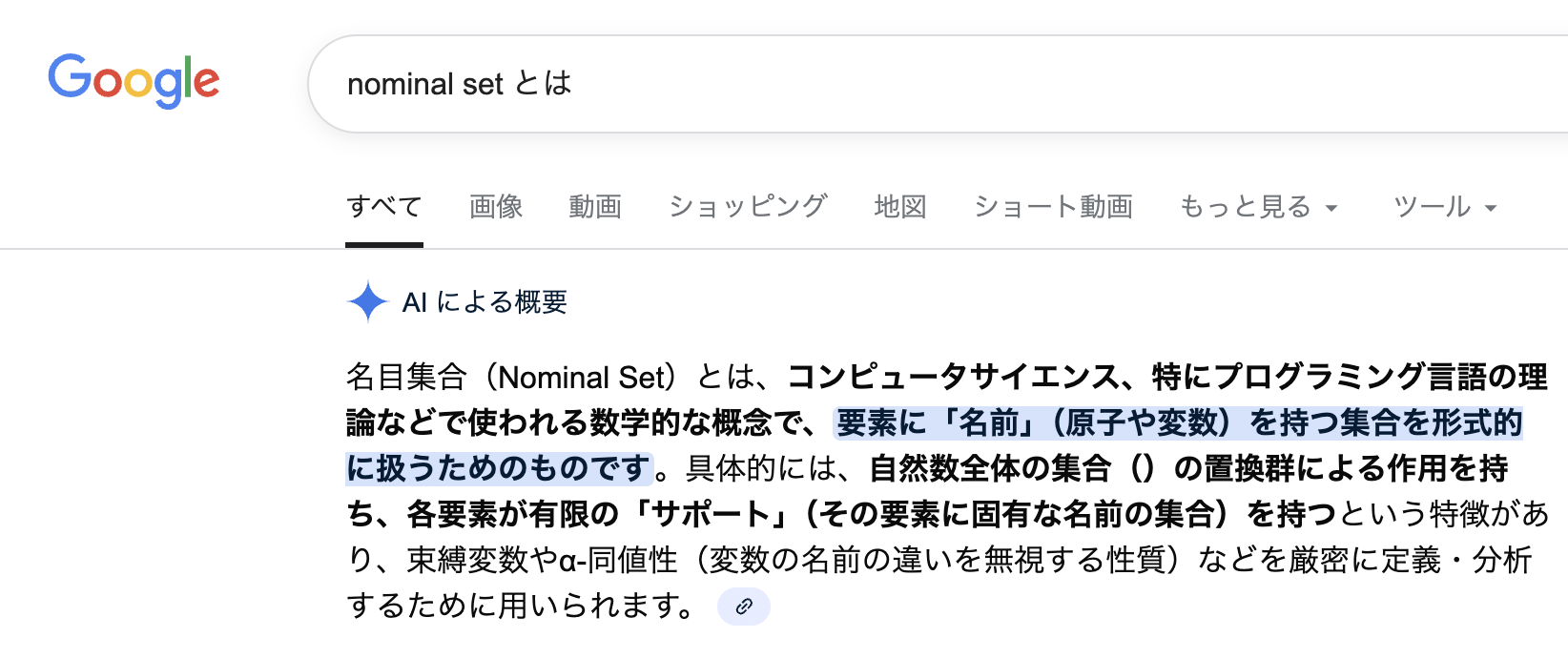
AI要約でnominal setが「名目集合」と訳されている。本当にやめてほしい。
また、少数ですが日本語で始めから書かれた論文でも名義アプローチの意味で『名目』という語を使っているものがあるようです。 これらは定訳が存在しない中で、著者の先生方が苦心して仮の訳語(あるいは経済学などの既存訳)を当てられたものと推察します。
- 山上 隼司、菊池 健太郎、上野 雄大、大堀 淳「アトム変数を用いた名目単一化の実装」 (2021, PDF)
- 鈴木 貴樹、菊池 健太郎、青戸 等人、外山 芳人「名目書き換えシステムの合流性について」 (2014, PDF)
- 菊池 健太郎「名目書き換えにおける強可換性を用いた合流性証明」 (2020, PDF)
ただし、まだ『名目』が定まった訳になっている、というわけでは無いと自分は考えています。 今ならまだ間に合うので、こうした論文の著者の先生方と連絡を取って、nominalを『名義』と訳すことについて議論し、新たな定訳として合意形成を図ることを、まずは第一の目標としていきます。
まとめ・結論
この記事では計算機科学の分野のnominalアプローチで見られる "nominal" という単語の適切な訳語を、他のアカデミックの分野での "nominal" の訳を調査して、検討しました。 そして、統計学の分野の名義尺度 (nominal scale) との理論的背景のレベルでのつながり (置換によって特徴付けられる名前) を発見しました。
結論としては、nominalアプローチの "nominal" は『名義』と訳されるべきです。
もちろん、訳語に正解があるわけではなく、どのような訳を選ぶべきかは個人の自由ではあります。 ただ、今回の名義尺度とnominalアプローチの関係性は避けて通れない点だと考えています。
今回の調査は個人的にも学びが多く、アカデミックな活動をしているという実感がありました。 意味の異なる "nominal" の使い方について、逐一別の訳を考えた先人達には全く頭が上がりません。 統計学 (そして心理学) において、nominal scaleが「名目尺度」や「公称尺度」ではなく「名義尺度」と訳されたことは、決して偶然ではなく、先人達のたゆまぬ努力の賜物なのだと信じています。
もしnominalアプローチに関心を持たれて、日本語で紹介や研究をする際は、『名義』という訳を使っていただけると非常に嬉しく思います。 また、この記事がnominalアプローチを日本で広める際の助けになれば、とも思います。
それでは、最後まで目を通していただきありがとうございました。
更新履歴
- 2026/01/15 (#e01b6a8): 第一版の公開。
- 2026/01/18 (#bd38696): 議論の流れなどを見直し全面的に書き直した第二版の公開。
- 2026/01/25: α変換の定義の見直し、名前的型システムへの言及などを含んだ第三版の公開。
脚注
-
機械翻訳なのではないかと思います。 ↩
-
nominalアプローチはFM集合論 (Fraenkel-Mostowski model) に由来するため、FM集合論の言葉 (atomやsupportなど) が伝統的に用いられています。 ↩
-
具体的には、すべての について となる置換 のことです。ここで、 は、単に置換の適用 です。 ↩
-
supportは任意に大きく取ることができるので、正確には「最小 (least) support」です。 任意の元が有限supportを持つなら、最小のsupportを取ることができることが知られています ([Gabbay & Pitts (2002)] のProposition 3.4)。 ↩
-
ネジや歯車などについてはnominal diameterも、nominal sizeと同様に「呼び径」と言うことがあるようです。 ↩
-
「型システム入門」§19.3より引用。 ↩
-
2026/01/24現在で、検索結果に出てきたのは次の9つのWebページです (検索結果1 / 検索結果2 / 検索結果3、検索結果4 / 検索結果5 / 検索結果6 / 検索結果7 / 検索結果8 / 検索結果9)。 ↩
-
こちらも私見ですが、唯名は衒学的で、却って学術的じゃないように思います。 ↩