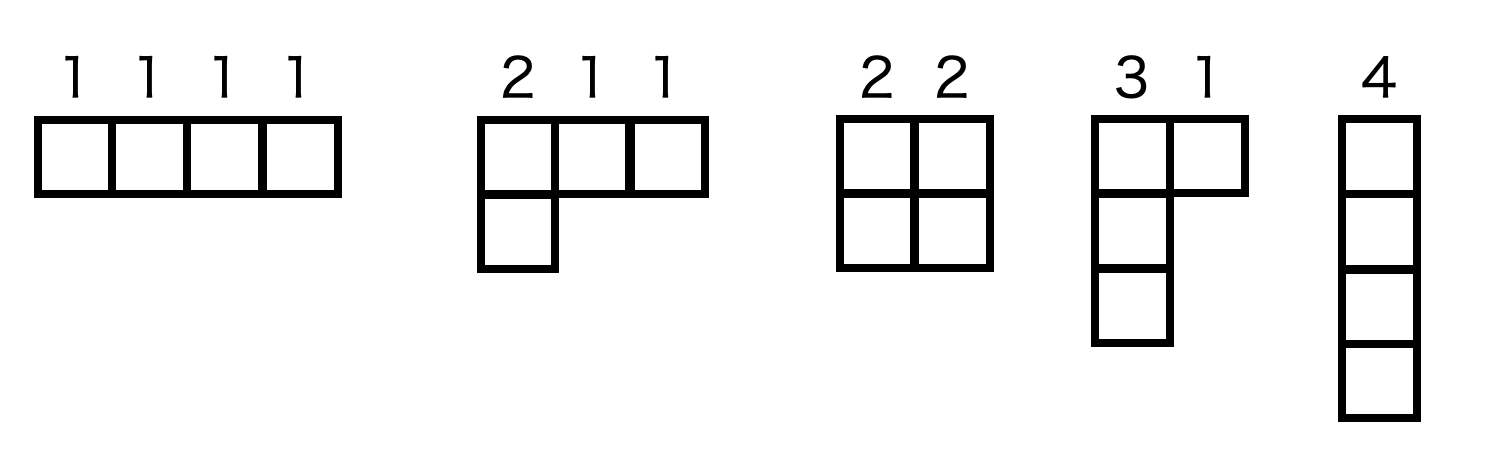自然数の分割とは、ある数と和が等しくなるような自然数の多重集合です。 例えば $\{\!| 3, 2, 2, 1 |\!\}$ は $3 + 2 + 2 + 1 = 8$ なので $8$ の分割となります。

この記事では、自然数の分割の積の最大値について考えます。

自然数の分割とは

自然数の分割とは、ある数と和が等しくなるような自然数の多重集合です。 例えば、$\{\!| 3, 2, 2, 1 |\!\}$ は $3 + 2 + 2 + 1 = 8$ なので $8$ の分割で、$\{\!| 7, 5, 2 |\!\}$ は $7 + 5 + 2 = 14$ なので $14$ の分割です。 また、ある数 $n$ について単一の集合 $\{\!| n |\!\}$ は $n$ 自身の分割になります。

数学の諸分野で、これが研究対象となります。 分かりやすいのは離散数学での数え上げで、自然数$4$の数え上げは次の5種類になります。

$$\{\!| 1, 1, 1, 1 |\!\},\, \{\!| 2, 1, 1 |\!\},\, \{\!| 2, 2 |\!\},\, \{\!| 3, 1 |\!\},\, \{\!| 4 |\!\}$$

この分割の、各自然の値だけ列に丸記号を置いて図示すると、次のようになります。

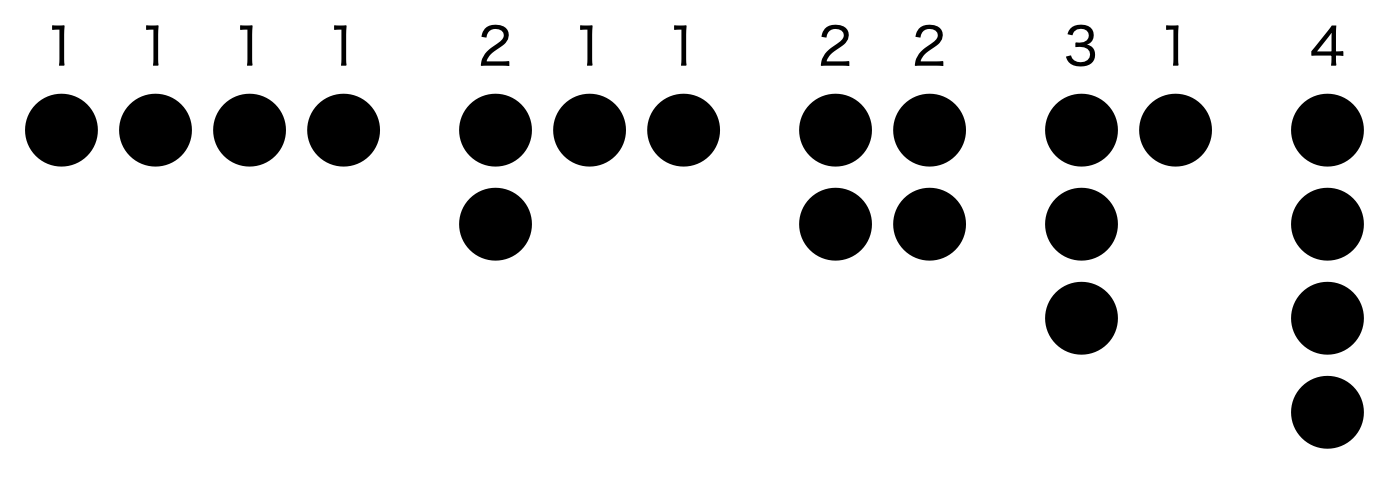
この図を見ると、4の分割は$\{\!| 1, 1, 1, 1 |\!\}$と$\{\!| 4 |\!\}$、$\{\!| 2, 1, 1 |\!\}$と$\{\!| 3, 1 |\!\}$がそれぞれ対称になっているというのが見てとれるのではないかと思います。 このような図はフェラーズ図形と呼ばれ、自然数の分割の考察に用いられてきました。

他にも丸記号を四角形にしたものはヤング図形と呼ばれます。

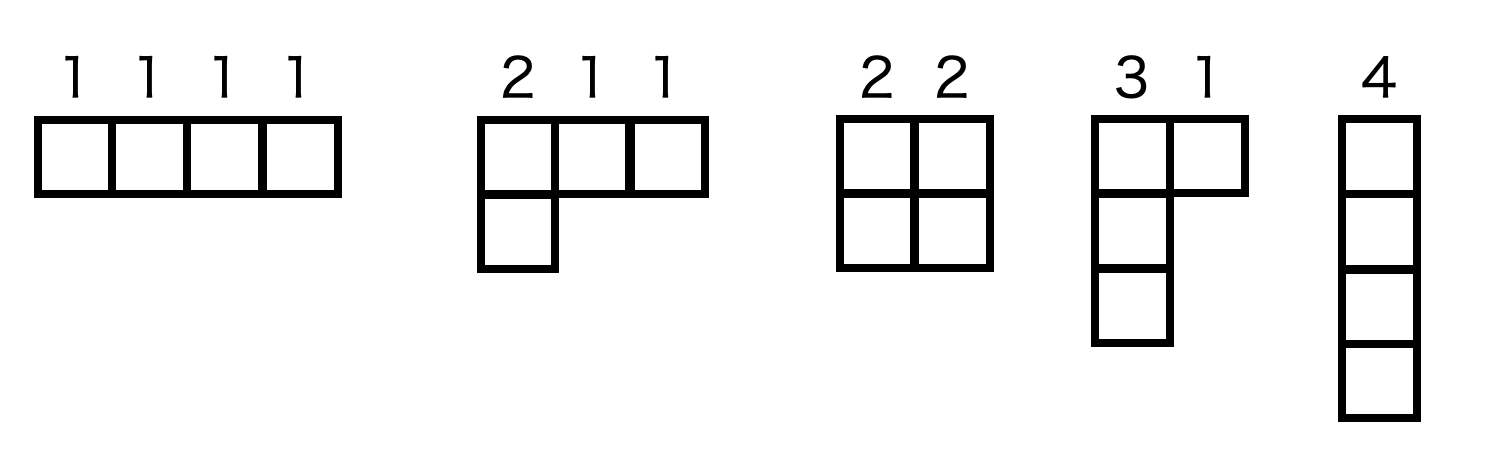
こちらの場合は、四角の中に数を書き込むことでより複雑な数学的構造を表現でき、群論の研究などで用いられることがあるらしいです。

この分割の数え上げの数列はOEISにA000041として登録されていて、その値は$n=0$から順に次のようになっています。

$$1, 1, 2, 3, 5, 7, 11, 15, 22, 30, \dots$$

OEISのページには色々なことが書かれていて、一度見てみると面白いです。

このように、自然数の分割は数学的に興味深い対象となっています。 そして、今回はこの自然数の分割の積の最大値について考えていきたいと思います。

積の最大値

自然数の分割の積とは、書いて字の通り分割の値をすべて掛けたものになります。 例えば$\{\!| 3, 2, 2, 1 |\!\}$は$8$の分割ですが、その積は$3 \times 2 \times 2 \times 1 = 12$となります。

そして「この積が最大となるような分割を見つけたい」というのが今回の記事の主題になります。

さて、あまり考えなくても、積が最大となる分割には「$1$が含まれることはない」ということは分かります。 というのも、ある自然数$n$について、$n$の分割が$\{\!| x_1, x_2, \cdots, x_k |\!\}$で$x_1 = 1$のとき、

$$x_1 + x_2 + x_3 + \cdots + x_k = (x_1 + x_2) + x_3 + \cdots + x_k = n$$

ですが、$x_1 \times x_2 < x_1 + x_2$なので、$\{\!| x_1 + x_2, x_3, \cdots, x_k |\!\}$の方が積の大きい分割となってしまうためです。 もっと単純に、$1$は掛けるよりも足した方が値を大きくできる数だから、と考えても良いです。

次に、もう少し考えると、積が最大となる分割には「$5$以上の数字が含まれることはない」ということも分かります。 同様に、$n$の分割が$\{\!| x_1, x_2, \cdots, x_k |\!\}$で$x_1 \ge 5$のとき、

$$x_1 + x_2 + x_3 + \cdots + x_k = (x_1 - 3) + 3 + x_2 + x_3 + \cdots + x_k = n$$

ですが、$x_1 < (x_1 - 3) \times 3$なので、$\{\!| x_1 - 3, 3, x_2, \cdots, x_k |\!\}$の方が積の大きい分割となるためです。

これらの考察から、積が最大となる分割には$2, 3, 4$のみで構成されていることが分かります。 さらに$2 \times 2 = 2 + 2 = 4$なので$4$を$2$を2個分と考えても差し支えないため、積が最大となる分割は$2$か$3$のみで構成されていると言うこともできます。 そして、可能な限り$2$ではなく$3$を掛けた方が積は大きくなります。

ここまで来れば、あとは$n$を$3$で割った余りについて場合分けすれば、積の最大値について一般項$P(n)$が求められます。

$$P(n) = \begin{cases} 3^{\frac{n}{3}} & \text{(if $n \equiv 0 \bmod 3$)} \\ 3^{\frac{n - 1}{3} - 1} \times 2^2 & \text{(if $n \equiv 1 \bmod 3$)} \\ 3^{\frac{n - 2}{3}} \times 2 & \text{(if $n \equiv 2 \bmod 3$)} \end{cases}$$

この値を素因数分解すれば、積が最大となる分割を得ることができます。

この数列はOEISのA000792として登録されています。 これは$n=0$から順に、次のようになります。

$$1, 1, 2, 3, 4, 6, 9, 12, 18, 27, \dots$$

結局何が言いたいのかと言うと$P(n)$の値は$n$について多項式で抑えることができず、指数的になるということです。 これが少し不思議なことに感じたので、今回記事にしてみました。

まとめ

自然数の分割に関しては、調べてみるともっと面白い話が色々ある気がします。 その辺りももう少し勉強したいと思っています。

最後まで目を通していただきありがとうございました。