Pike VMとEarley法の関係についてRubyで実装して考えてみる
正規表現マッチングの実装手法の1つとしてPike VMと呼ばれるものがあります。
これはGo言語の正規表現実装やRustのregex crateで使われている手法であり、正規表現と入力文字列に対しての計算量でマッチングができるのが特徴です。
Earley法はJay Earleyの提案した文脈自由文法 (CFG) の構文解析手法の1つです。 すべてのCFGを構文解析できる手法で最悪計算量はですが、無曖昧であればで、決定的であればで構文解析ができます。
実装してみると分かりますが、Pike VMとEarley法には類似している点があり、Earley法をPike VMの発展系のように考えることができます。 この記事ではPike VMとEarley法のRubyでの実装を通じて、それらの関係を解説します。
想定読者: 形式言語や構文解析についての基本的な知識がある (NFAやCFGなどを知っている) ことを想定しています。
Pike VM
Pike VMは正規表現マッチングの実装手法の1つです。
Rob Pikeがsamというテキストエディターの開発の際に実装した正規表現実装のアイディアが元となっている1ため、この名前で呼ばれています。
正規表現は非決定性有限状態オートマトン (NFA) に変換されてマッチングが実行されるため、正規表現マッチングとは結局のところ、いかにしてNFAの非決定的な動作を模倣するかという問題になります。 NFAの非決定的な動作を模倣する方法は、大きく分けて2つの方法が知られています。
1つはバックトラックを用いて逐次的に非決定的な遷移を模倣する方法です。 これは多くの正規表現エンジン (PCREやOnigmoなど) で用いられている方法となっています。
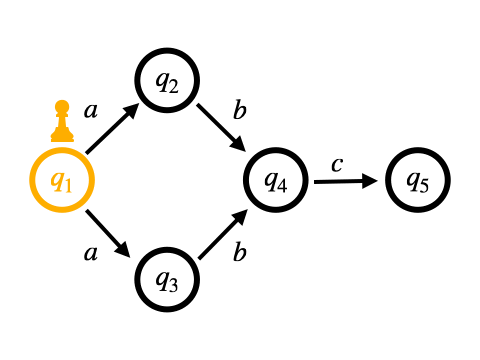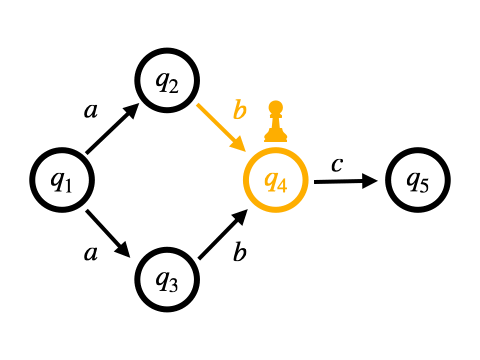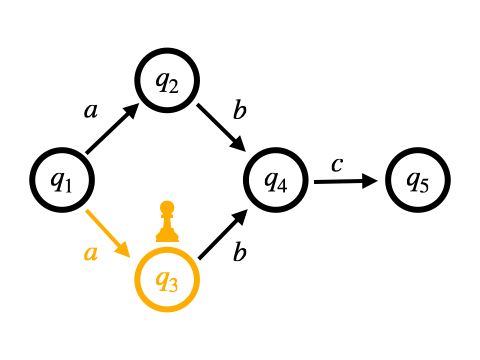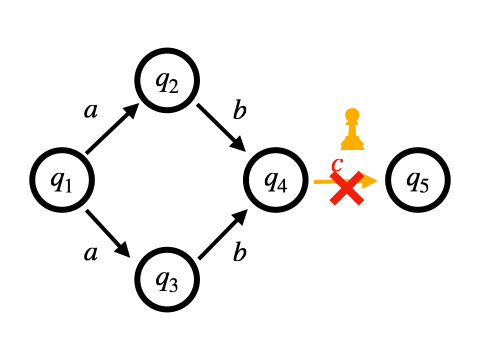
もう1つは、非決定的な遷移をすべて同時に行う方法です。 これはバックトラックを用いません。 NFAからDFAへの変換をマッチングをしながら行なっていくような動作のため、On-the-fly構成と呼ばれます。
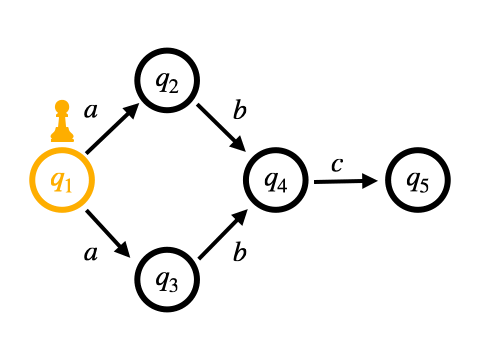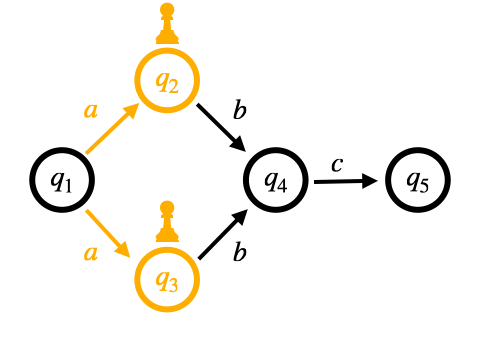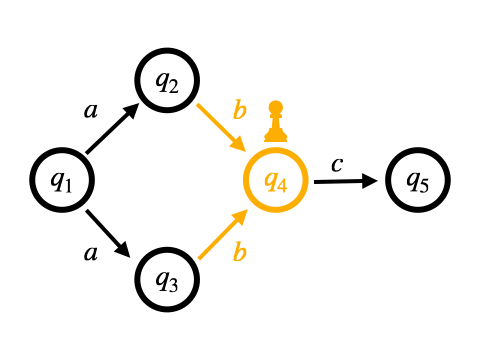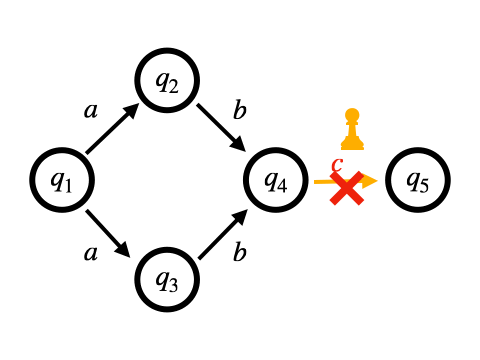
Pike VMはOn-the-fly構成に基づくマッチング手法となっています。
ここからはPike VMについて説明しながら、Pike VMをRubyで実装していきます。
Pike VMでのNFA
Pike VMはVMという名前の通りVMによってマッチングを行ないます。 そのため、正規表現はVMの命令列に変換されるのですが、実はそれらの命令はNFAの辺とラベルとして理解する方が分かりやすいです。 そこで、VMの命令をNFA風の図で説明します。
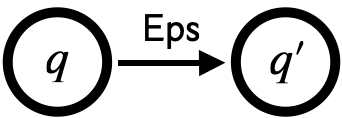
Pike VMの命令は4種類あります。
-
: 空文字列でに遷移できる
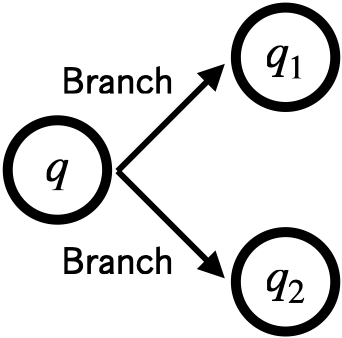
-
: 空文字列でかに遷移できる
-
: 文字でに遷移できる
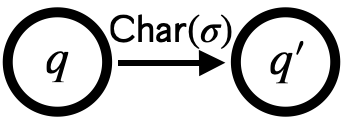
-
: 受理状態を表す
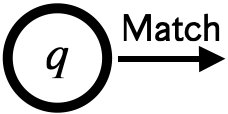
これらの命令のデータ型をRubyで定義します。
Eps = Data.define(:to)
Branch = Data.define(:to1, :to2)
Char = Data.define(:char, :to)
Match = Data.define()さらに、これらを使ったPike VMでのプログラム (NFA) も定義しておきます。
NFA = Data.define(:initial, :transition)この定義で図のNFA (/a*/に対応するNFA) を表現すると、次のコードのようになります。
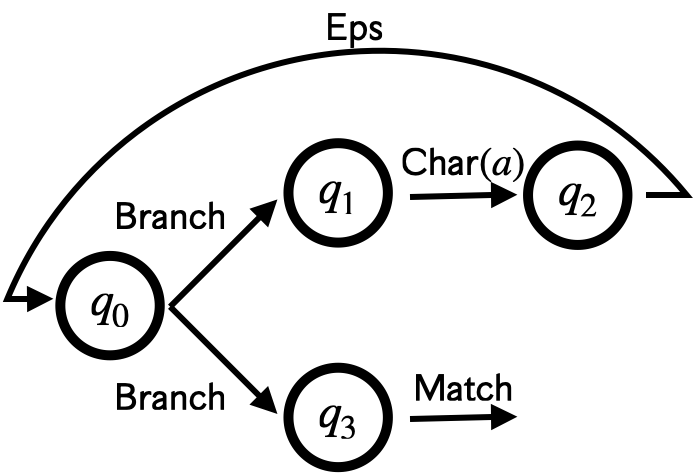
example_nfa = NFA[
0,
{
0 => Branch[1, 3],
1 => Char['a', 2],
2 => Eps[0],
3 => Match[]
}
]正規表現からPike VMのNFAへの変換
Pike VMが正規表現マッチングを行なえることを確認するために、正規表現からPike VMへの変換を実装しておきます。
最初に、正規表現を表すデータ型を定義します。
Cat = Data.define(:left, :right)
Alt = Data.define(:left, :right)
Rep = Data.define(:node)
Lit = Data.define(:char)この型を使って/a*|ab/を表すには次のようにします。
example_regex = Alt[Rep[Lit['a']], Cat[Lit['a'], Lit['b']]]この型からPike VMのNFAへの変換は次のようなコードで出来ます。
module ToNFA
protected def to_nfa_loop(transition)
case self
in Cat[l, r]
q10, q11 = l.to_nfa_loop(transition)
q20, q21 = r.to_nfa_loop(transition)
transition[q11] = Eps[q20]
[q10, q21]
in Alt[l, r]
q10, q11 = l.to_nfa_loop(transition)
q20, q21 = r.to_nfa_loop(transition)
q0, q1 = transition.size, transition.size + 1
transition[q0] = Branch[q10, q20]
transition[q11] = Eps[q1]
transition[q21] = Eps[q1]
transition[q1] = Match[]
[q0, q1]
in Rep[r]
q10, q11 = r.to_nfa_loop(transition)
q0, q1 = transition.size, transition.size + 1
transition[q0] = Branch[q10, q1]
transition[q11] = Eps[q0]
transition[q1] = Match[]
[q0, q1]
in Lit[a]
q0, q1 = transition.size, transition.size + 1
transition[q0] = Char[a, q1]
transition[q1] = Match[]
[q0, q1]
end
end
def to_nfa
transition = {}
q0, _ = to_nfa_loop(transition)
NFA[q0, transition]
end
end
[Cat, Alt, Rep, Lit].each do |klass|
klass.include(ToNFA)
end変換結果はこんな風になります。
pp example_regex.to_nfa
# => #<data NFA
# initial=8,
# transition=
# {0=>#<data Char char="a", to=1>,
# 1=>#<data Eps to=2>,
# 2=>#<data Branch to1=0, to2=3>,
# 3=>#<data Eps to=9>,
# 4=>#<data Char char="a", to=5>,
# 5=>#<data Eps to=6>,
# 6=>#<data Char char="b", to=7>,
# 7=>#<data Eps to=9>,
# 8=>#<data Branch to1=2, to2=4>,
# 9=>#<data Match>}>Pike VMの実装
それではPike VMの実装をします。
最初に書いたとおり、Pike VMはOn-the-fly構築を用いてマッチングを行ないます。 具体的には、次のような流れになります。
- 0文字目のキューに初期状態を追加
- 現在の文字のキューから状態を読み込み、その状態の命令 (遷移) を実行
Eps[q]: 現在の文字のキューにqを追加Branch[q1, q2]: 現在の文字のキューにq1, q2を追加Char[a, q]: 現在の文字がaなら、次の文字のキューにqを追加
- キューから読み込む状態が無くなるまで2を繰り返す
- 文字を進めて次のキューで2と3を繰り返す
- 最後のキューに命令が
Matchの状態が残っていたらマッチと判定
つまり、空文字列で遷移できる部分を可能な限り遷移して、命令による遷移で次の文字に移動する、というのを幅優先探索の要領で繰り返していきます。
これをコードにします。
class PikeVM
def initialize(nfa, input)
@nfa = nfa
@input = input
@queues = Hash.new { |hash, index| hash[index] = [] }
end
def run
enqueue 0, @nfa.initial
(0..@input.size).each do |pos|
step pos
end
@queues[@input.size].any? { |q| @nfa.transition[q].is_a?(Match) }
end
private def step(pos)
# `@queues[pos]`は実行中に要素が増えていくことに注意
@queues[pos].each do |q|
case @nfa.transition[q]
in Eps[q1]
enqueue pos, q1
in Branch[q1, q2]
enqueue pos, q1
enqueue pos, q2
in Char[a, q1]
next unless @input[pos] == a
enqueue pos + 1, q1
in Match[]
# nothing
end
end
end
private def enqueue(pos, q)
# すでに`@queues[pos]`に`q`が追加されていない場合に`q`を追加する
return if @queues[pos].include?(q)
@queues[pos].push(q)
end
endこのPikeVMクラスにNFAとマッチングしたい文字列を渡して、runメソッドを呼ぶとマッチングが実行されます。
# `example_regex`は`/a*|ab/`
p PikeVM.new(example_regex.to_nfa, "ab").run # => true
p PikeVM.new(example_regex.to_nfa, "ba").run # => false
p PikeVM.new(example_regex.to_nfa, "aaaa").run # => trueこのPikeVMのマッチングの計算量が、正規表現と入力文字列に対してとなる理由は次の通りです。
- NFAの状態数は正規表現の大きさに比例する。
- 各キューに追加されうる要素はたかだか種類なので
stepのeachの繰り返し回数は。 runの中で回stepを呼び出すので、全体の計算量は。
というわけで、文字列の長さに線形に比例する計算量でマッチングが実装できることが分かりました。
Earley法
次はEarley法について説明します。 Earley法はJay Earleyが1968年に提案したCFGの解析手法の1つ2です。 解析の最悪計算量はですが、文法が無曖昧な場合はで、決定的な場合はで解析できることが知られています。 さらに、少し方法を修正することで、任意の文法についてで解析できることも知られています3。
実はEarley法は、Pike VMによるマッチングをProcedural Automatonに拡張したものと考えることができます。 Procedural AutomatonやPike VMをこれに対応するために拡張する方法について説明していきます。
Procedural Automaton
Procedural Automatonとは、「他のオートマトンを呼び出すことができる」オートマトンの拡張で、呼び出すオートマトンをすべてまとめた複数のオートマトンのまとまりをSystem of Procedural Automata (SPA)と呼びます45。 SPAはCFG全体を表現できる力があることが知られています。
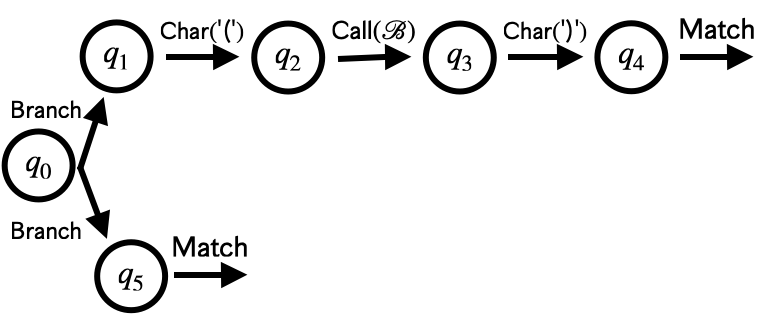
例えば次の図のSPAは、"({()})({})"のような(...)と{...}が交互に入れ子になって並んでいる場合にマッチするオートマトンとなっています。

というのがProcedural Automatonのために追加された新しい命令で、を呼び出して、マッチした場合にに遷移します。 例でもあるように、この呼び出しは再帰的に行なうことができ、それによってCFGを表現できます。
RubyでもCall命令と、SPAを表すデータ型を定義しておきます。
Call = Data.define(:name, :to)
SPA = Data.define(:start, :nfa)このデータ型を使って、さきほどの例を表現すると次のようになります。
nfa_a = NFA.new(
0,
{
0 => Branch[1, 5],
1 => Char['(', 2],
2 => Call[:B, 3],
3 => Char[')', 4],
4 => Eps[0],
5 => Match[]
}
)
nfa_b = NFA.new(
0,
{
0 => Branch[1, 5],
1 => Char['{', 2],
2 => Call[:A, 3],
3 => Char['}', 4],
4 => Eps[0],
5 => Match[]
}
)
spa_example = SPA.new(
:A,
{
A: nfa_a,
B: nfa_b
}
)CFGからSPAへの変換
CFGの1つの生成規則を正規表現の文字の並び、複数の生成規則を|による分岐と見做せば、CFGをオートマトンに変換することは難しくありません。
例えば、次のようなCFGの文法があったとします。
このときに対応するオーマトンは次のような一直線のものになります。

そして、の2つの生成規則 ( と ) をまとめたものは次のようになります。
CFGの文法を表すデータ型をこのように定義します。
Term = Data.define(:value)
NonTerm = Data.define(:name)
Rule = Data.define(:name, :symbols)
Grammar = Data.define(:rules)
# 例をこのデータ型で表現したもの
grammar = Grammar[[
Rule[:A, [Term['('], NonTerm[:B], Term[')']]],
Rule[:A, []],
Rule[:B, [Term['{'], NonTerm[:A], Term['}']]],
Rule[:B, []],
]]このCFGの文法からSPAへの変換は次のように実装できます。
class Grammar # `Grammar`クラスを拡張
def to_spa
symbols_to_transition = ->(transition, symbols) {
q0 = transition.size
symbols.each do |s|
q1, q2 = transition.size, transition.size + 1
case s
in Term[a]
transition[q1] = Char[a, q2]
in NonTerm[x]
transition[q1] = Call[a, q2]
end
end
q1 = transition.size
transition[q1] = Match[]
q0
}
start = rules.first.name
nfa = {}
rules.group_by(&:name).each do |name, rules|
transition = {}
q0 = symbols_to_transition.(transition, rules[0].symbols)
rules[1..].each do |rule|
q1 = symbols_to_transition.(transition, rule.symbols)
transition[transition.size] = Branch[q0, q1]
q0 = transition.size - 1
end
nfa[name] = NFA.new(q0, transition)
end
SPA.new(start, nfa)
end
end
pp grammar.to_spa
# => #<data SPA
# start=:A,
# nfa=
# {:A=>
# #<data NFA
# initial=5,
# transition=
# {0=>#<data Char char="(", to=1>,
# 1=>#<data Call name=nil, to=2>,
# 2=>#<data Char char=")", to=3>,
# 3=>#<data Match>,
# 4=>#<data Match>,
# 5=>#<data Branch to1=0, to2=4>}>,
# :B=>
# #<data NFA
# initial=5,
# transition=
# {0=>#<data Char char="{", to=1>,
# 1=>#<data Call name=nil, to=2>,
# 2=>#<data Char char="}", to=3>,
# 3=>#<data Match>,
# 4=>#<data Match>,
# 5=>#<data Branch to1=0, to2=4>}>}>Pike VMの拡張
Pike VMを命令に対応させるためには、まず、キューに追加する情報を状態だけでなく3つ組[name, q, start_pos]に修正する必要があります。
これらはそれぞれ、次のような値になります。
name: 現在呼び出されているオートマトンの名前q: 現在のオートマトンの状態start_pos: このオートマトンを呼び出しはじめた文字列上の位置
nameとqは命令を読み込むために必要です。
start_posは、これがあることによってオートマトンにマッチしたときに呼び出し元に戻って、次の状態に行けます。
このように拡張したPike VMをEarleyVMという名前で実装します。
class EarleyVM
def initialize(spa, input)
@spa = spa
@input = input
@queues = Hash.new { |hash, index| hash[index] = [] }
end
def run
enqueue 0, @spa.start, @spa.nfa[@spa.start].initial, 0
(0..@input.size).each do |pos|
step pos
end
@queues[@input.size].any? do |name, q, start_pos|
@spa.start == name &&
@spa.nfa[name].transition[q].is_a?(Match) && start_pos == 0
end
end
private def step(pos)
# `@queues[pos]`は実行中に要素が増えていくことに注意
@queues[pos].each do |name, q, start_pos|
case @spa.nfa[name].transition[q]
in Eps[q1]
enqueue pos, name, q1, start_pos
in Branch[q1, q2]
enqueue pos, name, q1, start_pos
enqueue pos, name, q2, start_pos
in Char[a, q1]
next unless @input[pos] == a
enqueue pos + 1, name, q1, start_pos
in Call[next_name, _]
enqueue pos, next_name, @spa.nfa[next_name].initial, pos
in Match[]
# `@queues[start_pos]`から命令が`Call[name, q1]`となっている状態を探し、
# 遷移を次に進める
@queues[start_pos].each do |old_name, old_q, old_start_pos|
case @spa.nfa[old_name].transition[old_q]
in Call[next_name, q1] if name == next_name
enqueue pos, old_name, q1, old_start_pos
else
# nothing
end
end
end
end
end
private def enqueue(pos, name, q, start_pos)
# すでに`@queues[pos]`に`[name, q, start_pos]`が追加されていない場合に
# `[name, q, start_pos]`を追加する
triple = [name, q, start_pos]
return if @queues[pos].include?(triple)
@queues[pos].push(triple)
end
endEarleyVMの使用例は次のようになります。
括弧のネストを正しく解釈できていることが分かります。
p EarleyVM.new(spa_example, "({()})()").run # => true
p EarleyVM.new(spa_example, "({(}))").run # => falseあとがき
というわけでPike VMとEarley法について解説しました。 NFAの非決定性を同時に遷移してシミュレートしていく方法の延長線でCFGを構文解析する、という考えがEarley法の発端だと思われます。 そのため、実装という観点から見るとEarley法がPike VMの拡張になるのも道理でしょう。
今回のPike VMの実装はEarley法の解説にスムーズにつなげるため、よくある実装とは少し異なった形になっています。 まず、すべての文字列上の位置のキューを保存していますが、Pike VMであれば現在のキューと次のキューの2つだけで十分です。 また、空文字列で遷移できる部分を一度にすべて遷移することで、キューに追加するのは命令と命令の状態だけで十分になります。
Earley法は、計算量的にはLR法にも負けず劣らずのアルゴリズムなのですが、実際に実装してみると途中に生成する (キューに追加する) オブジェクトの生成がボトルネックになって、想像よりも遅くなりがちです。 また、今回は実装しませんでしたが、実際に利用するためには構文解析後に構文木を構築する必要があります。 そのためのデータ構造など、工夫できる点は色々あるので、挑戦してみると面白いと思います。
最後まで目を通していただきありがとうございました。
脚注
-
Earley, Jay. "An efficient context-free parsing algorithm." Communications of the ACM 13.2 (1970): 94-102. (※ 最初に発表したのは1968年ですが、よりフォーマルな形で発表したのは1970年のようです) ↩
-
Leo, Joop MIM. "A general context-free parsing algorithm running in linear time on every LR (k) grammar without using lookahead." Theoretical computer science 82.1 (1991): 165-176. ↩
-
Frohme, Markus, and Bernhard Steffen. "Compositional learning of mutually recursive procedural systems." International Journal on Software Tools for Technology Transfer 23 (2021): 521-543. ↩
-
他にも同等のものをContext-Free Process SystemやRecursive State Machine (RSM) と呼ぶこともあるらしいです。 ↩